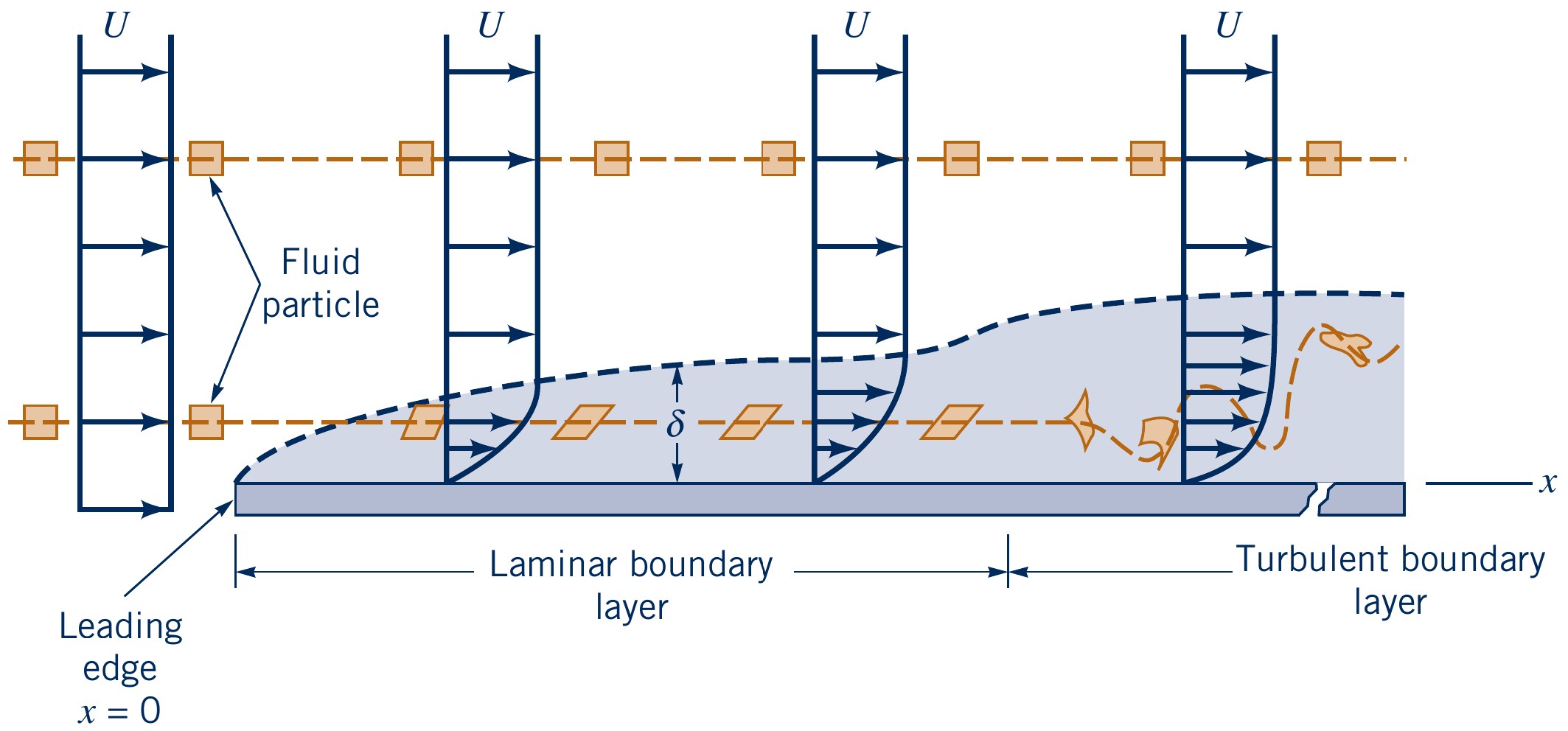
Boundary Layer Structure

Boundary layer (BL) structure and development for parallel flow over an infinite flat plate

• Only fluid in BL "feels" the plate
• $\text{Re}_x = \rho U x / \mu$ (bulk flow definition)

Laminar BL: Analytical expressions from Blasius BL solution

Turbulent BL: Mostly empirical expressions

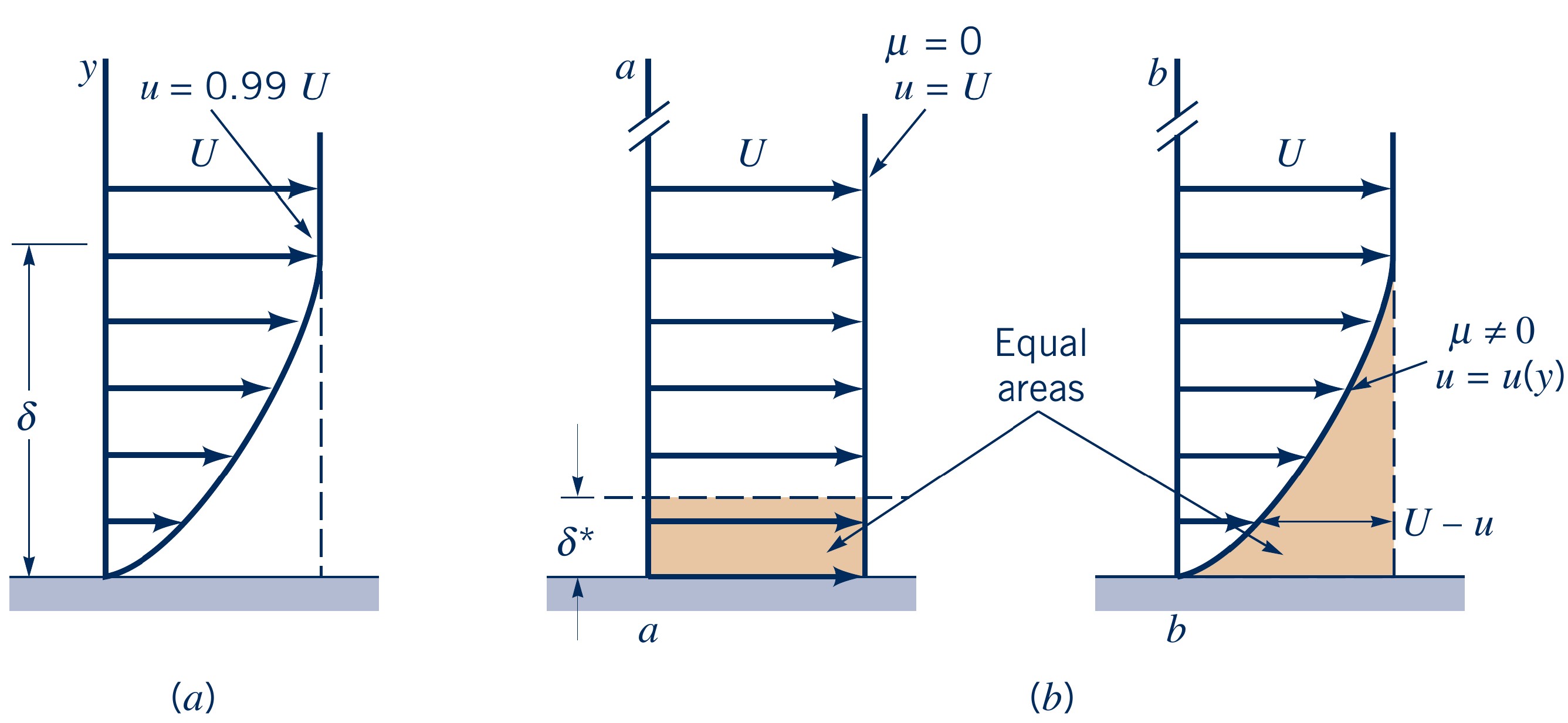
Boundary Layer Thickness

BL thickness definitions:

• Standard BL thickness $\delta_{99}=\delta$
• BL displacement thickness $\delta^*$
• BL momentum thickness $\Theta$

Excellent experiment showing turbulent BL triggered by trip wire in this classical flow case

• Note: Friction Reynolds number $\text{Re}_\tau=\frac{\rho \ \sqrt{\tau_w/\rho} \ \delta }{\mu}$ (local) rather than bulk Reynolds number $\text{Re}_x=\frac{\rho \ U \ x}{\mu}$ is used in video

Turbulent Shear Stress

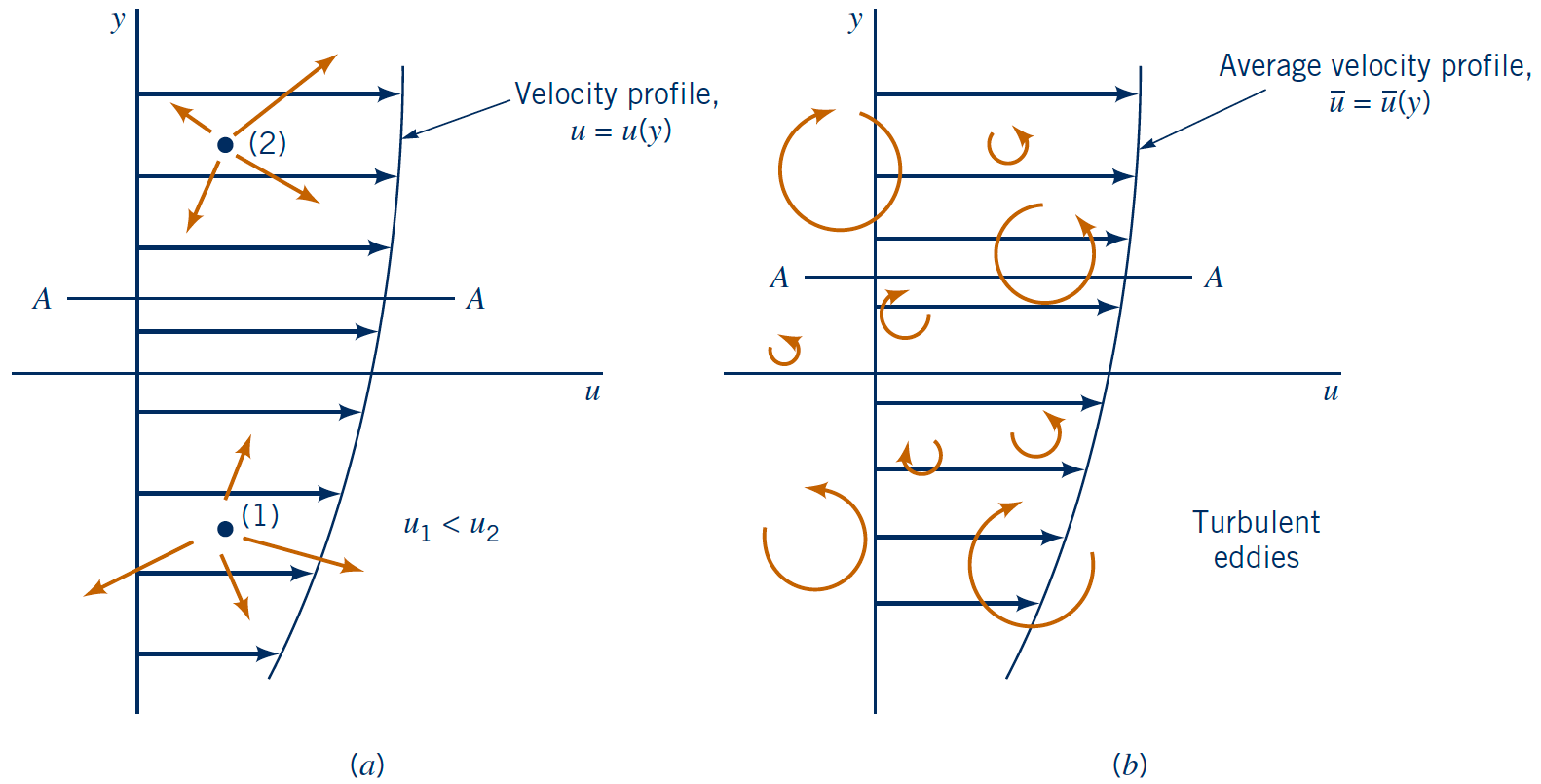
Recall how the instantaneous (horizontal) velocity $u$ could be decomposed into a time-averaged and fluctuating part (Reynolds decomposition):

$$u(x,y,z,t) = \overline{u}(x,y,z) + u'(x,y,z,t)$$

• Tempting to apply our Newtonian shear stress definition directly to $\overline{u}$ in turbulent BL
• However, $\tau \neq \mu \frac{d\overline{u}}{dy}$ (with turbulence)

Let us review the underlying physics:

• Laminar BL
  • Molecular diffusion
  • $x$-momentum transfer in $y$ due to $\frac{du}{dy} \neq 0$ → Shear stress
• Turbulent BL
  • Finite size 3-D eddies
  • Increasing momentum transfer
  • Extra term in shear stress: $$\tau = \mu \frac{d\overline{u}}{dy} - \rho \overline{u'v'} = \tau_{lam} + \tau_{turb}$$

Reynolds Stresses

The additional contribution to shear stress from fluctuations $\tau_{turb} = -\rho \overline{u'v'}$ has units of Pa and is termed Reynolds stresses.

• These stresses are flow dependent and difficult to describe
• Fluctuating velocities influence the mean flow
• Boussinesq hypothesis: $$\tau = \mu_t \frac{d\overline{u}}{dy}$$
• Shifts the problem from Reynolds stresses to $\mu_t$ (flow dependent scalar)
• The basis of widely used RANS and URANS turbulence models
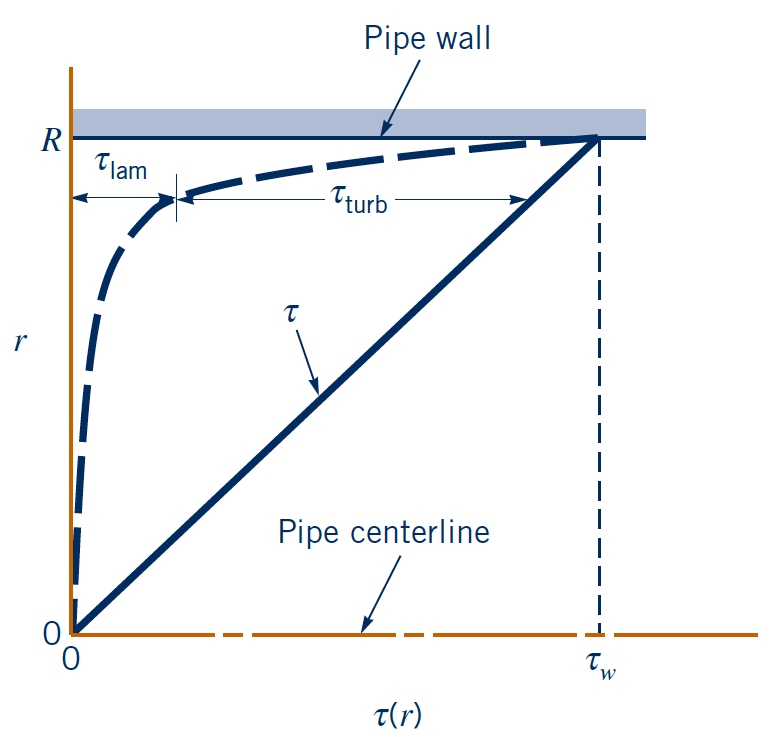
• Typical ratio of $\tau_{lam}$ and $\tau_{turb}$ in turbulent BL varies with distance to the wall (here for a pipe flow)

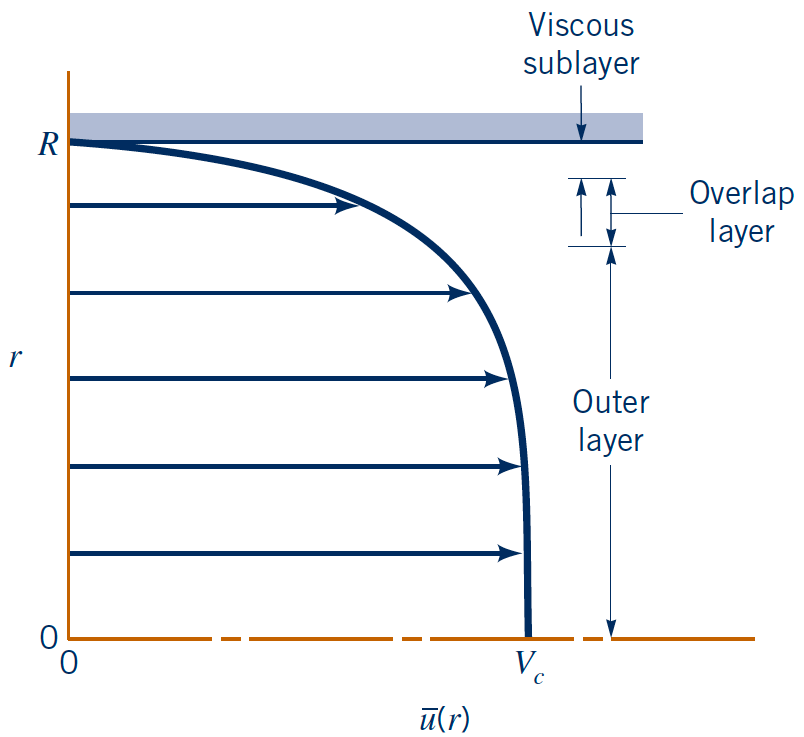
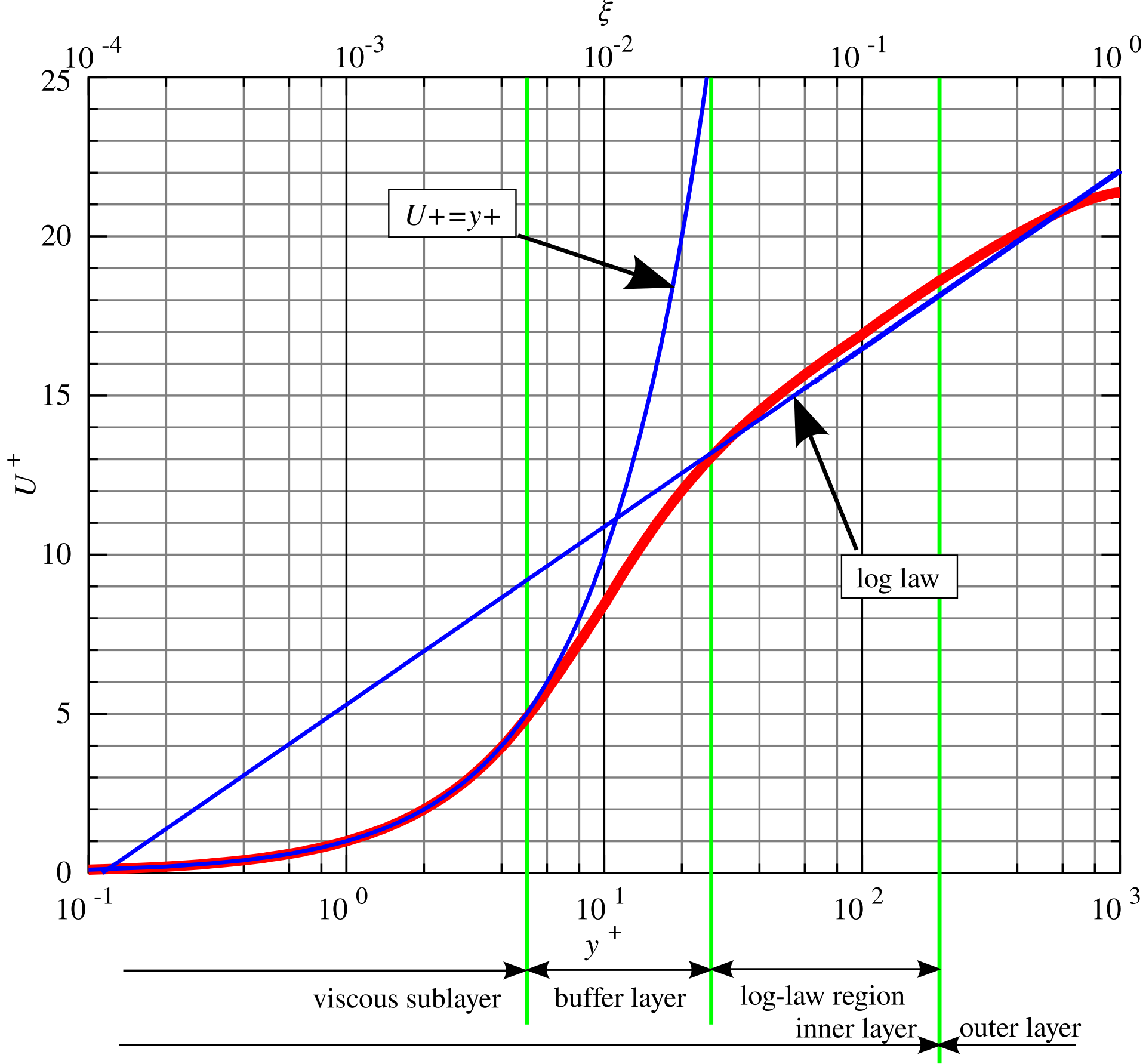
Turbulent Velocity Profile

Turbulent BL: Three regions with distinct physics given from distance to wall

• Dimensionless $y$ coordinate: $y^+ = y u^* / \nu$ with $u^* = \sqrt{\tau_w / \rho}$
• Dimensionless velocity: $u^+ = \overline{u} / u^*$

• Viscous sublayer ($y^+ < 5$)
  • Viscous forces dominant over Reynolds stresses
  • Smooth wall: $u^+ = y^+$
• Buffer layer ($5 < y^+ < 30$)
  • Both viscous sublayer and log law important (transition function)
• Log-law layer ($30 < y^+ < 200$)
  • Velocity varies as the logarithm of $y$
  • Experimentally determined (law of the wall): $$u^+ = \frac{1}{\kappa} \ln(y^+) + C^+$$
  • Where $\kappa$ is the von Kármán Constant: $\kappa=0.41$ and $C^+ = 5$ (for smooth walls and flow over infinite flat plate)

• Viscous sublayer extremely thin
• Roughness of the wall can enter viscous sublayer $\rightarrow$ changed $u(y)$